Commits on Source (13)
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
-
Nicolas Aspert authored
Showing
- environment.yml 2 additions, 1 deletionenvironment.yml
- exercises/week03/Projections and signal restoration.ipynb 471 additions, 0 deletionsexercises/week03/Projections and signal restoration.ipynb
- exercises/week03/images/pocs.png 0 additions, 0 deletionsexercises/week03/images/pocs.png
- exercises/week04/Deblurring.ipynb 364 additions, 0 deletionsexercises/week04/Deblurring.ipynb
- exercises/week05/Linear systems - Poisson equation.ipynb 290 additions, 0 deletionsexercises/week05/Linear systems - Poisson equation.ipynb
- exercises/week06/Recursive least squares.ipynb 554 additions, 0 deletionsexercises/week06/Recursive least squares.ipynb
- exercises/week06/data.npz 0 additions, 0 deletionsexercises/week06/data.npz
- exercises/week07/RBF networks.ipynb 395 additions, 0 deletionsexercises/week07/RBF networks.ipynb
- exercises/week07/images/RBF_NN.png 0 additions, 0 deletionsexercises/week07/images/RBF_NN.png
- solutions/week02/Linear transforms.ipynb 670 additions, 0 deletionssolutions/week02/Linear transforms.ipynb
- solutions/week03/Projections and signal restoration.ipynb 1264 additions, 0 deletionssolutions/week03/Projections and signal restoration.ipynb
- solutions/week03/images/pocs.png 0 additions, 0 deletionssolutions/week03/images/pocs.png
- solutions/week04/Deblurring.ipynb 1095 additions, 0 deletionssolutions/week04/Deblurring.ipynb
- solutions/week05/Linear systems - Poisson equation.ipynb 489 additions, 0 deletionssolutions/week05/Linear systems - Poisson equation.ipynb
- solutions/week06/Recursive least squares.ipynb 1477 additions, 0 deletionssolutions/week06/Recursive least squares.ipynb
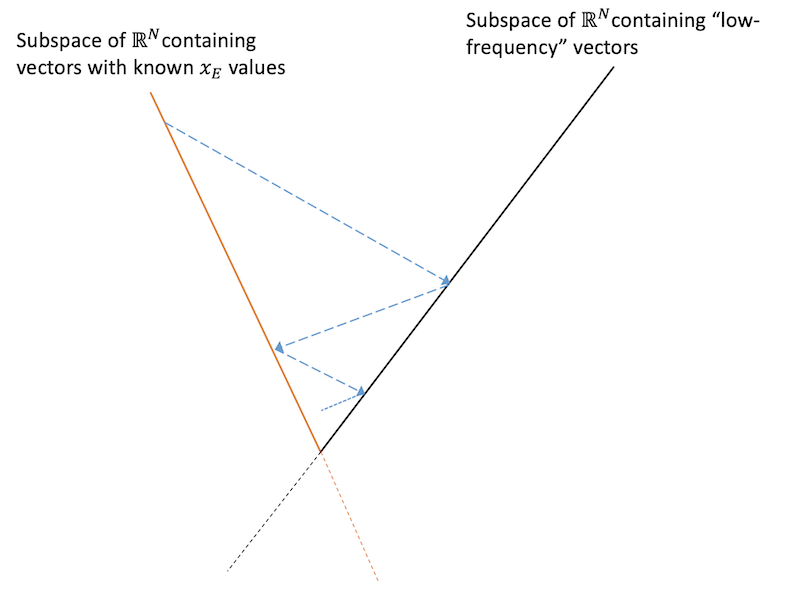
exercises/week03/images/pocs.png
0 → 100644
76.9 KiB
exercises/week04/Deblurring.ipynb
0 → 100644
exercises/week06/data.npz
0 → 100644
File added
exercises/week07/RBF networks.ipynb
0 → 100644
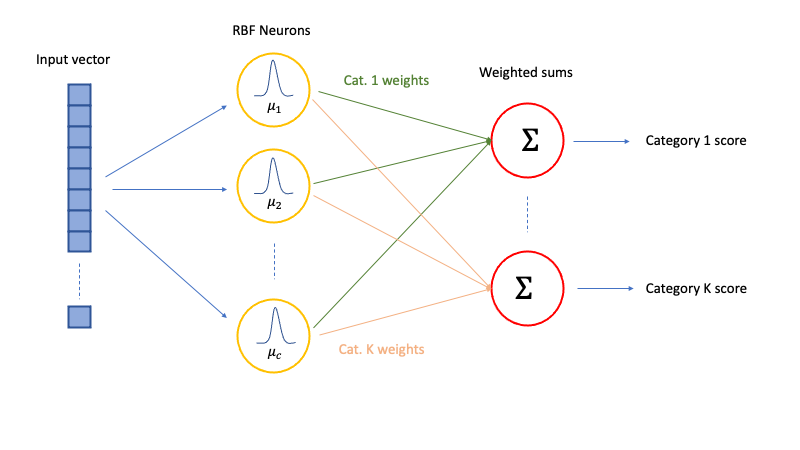
exercises/week07/images/RBF_NN.png
0 → 100644
47 KiB
solutions/week02/Linear transforms.ipynb
0 → 100644
Source diff could not be displayed: it is too large. Options to address this: view the blob.
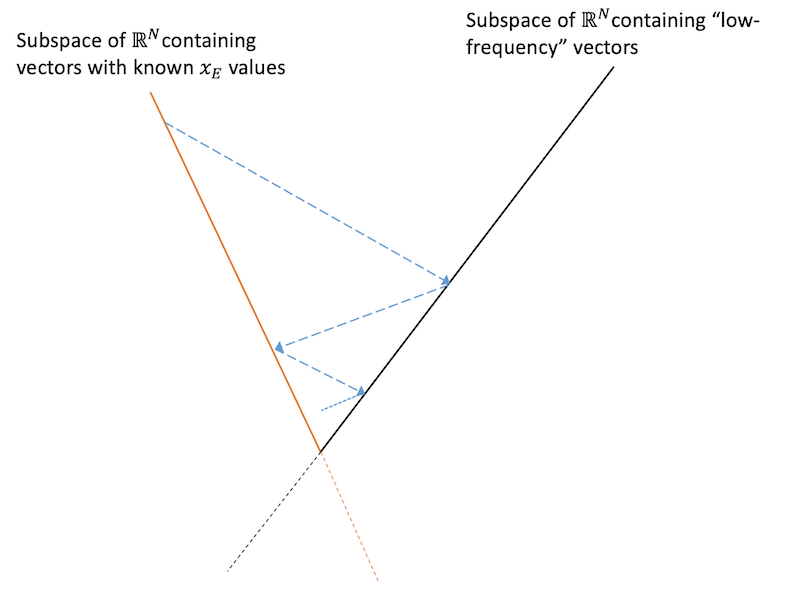
solutions/week03/images/pocs.png
0 → 100644
76.9 KiB
solutions/week04/Deblurring.ipynb
0 → 100644
Source diff could not be displayed: it is too large. Options to address this: view the blob.
Source diff could not be displayed: it is too large. Options to address this: view the blob.